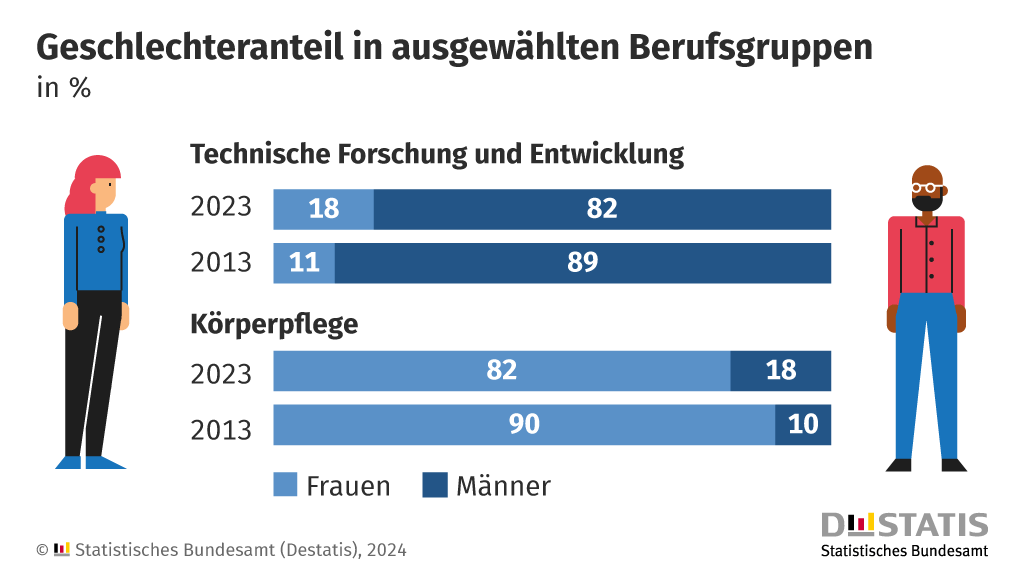
Frauen sind in der IT oder Forschung und Entwicklung nach wie vor unterrepräsentiert, Männer in Körperpflegeberufen oder im Verkauf von Lebensmitteln. Doch das ändert sich zunehmend. So ist der Frauenanteil in der technischen Forschung und Entwicklung im Jahr 2023 auf 18% gestiegen.